如何判断两条线段是否相交
前几天参加阿里的笔试,遇到了一道有趣的题目,题目大致意思是说有一个矩形墓室,入口的位置为(0,0),出口位置为(m,n)。墓室中散步着一些散光发射器,某些激光发射器之间有激光。m,n和激光的起始和终止位置(x1,y1,x2,y2)均为整数。请问能否在不碰到激光的情况下从入口走到出口。
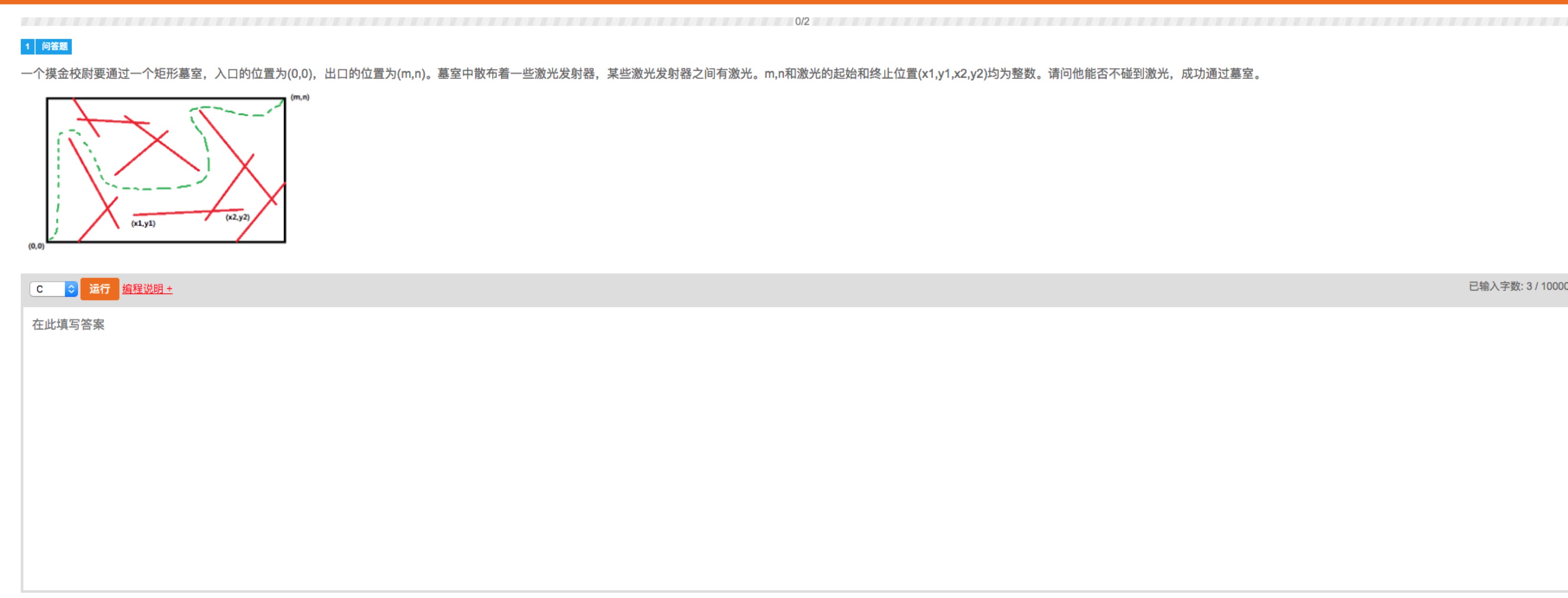
这道题不需要我们求解出路线,只需判定是否有解即可。可以通过将所有激光按照是否相互交叉分为几堆,对于每一堆分别考虑,若其堵住了从入口到出口的所有路(具体表现为横穿或纵穿整个墓室,或者占据左下角或右上角),则无解,否则总可以绕过这些激光。
上诉思路中最关键的部分就是判断两个线段是否有交点,这个问题初看简单,但是细想还是有很多问题需要考虑的,一不小心就会陷入各种特判。
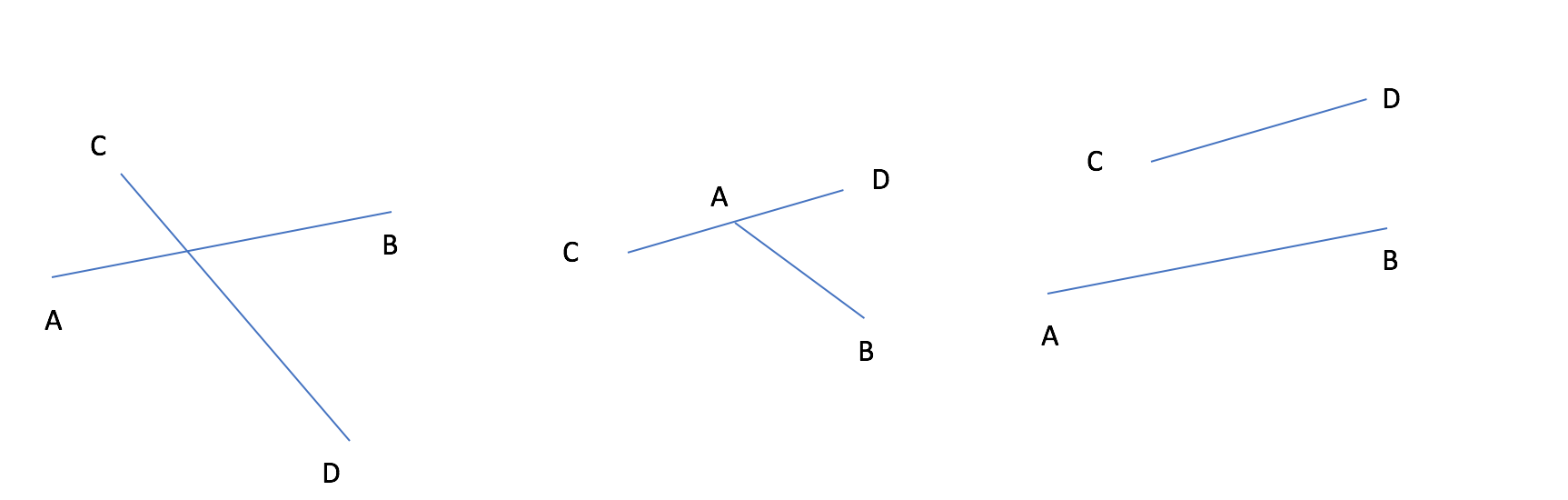
通过观察下图我们可以发现若AB,CD相交,则必有AB分列于CD两边(或者A/B在线段CD上),CD也同理,一旦AB位于CD的同一侧(CD同理),则AB,CD不可能相交。因此一个简单的判定方法就产生了:
$cross = ||AB \times AC|| \cdot ||AB \times AD|| \leq 0 \land ||CD \times CA|| \cdot ||CB \times CD||\leq 0 $
上面的判定方法几乎完美,可惜,只是“几乎”,有一种情况没法处理,那就是AB,CD共线但是不相交的情况,在这种情况下$||AB \times AC|| = ||AB\times AD|| = ||CD \times CA|| = ||CB \times CD|| = 0$。
解决方案就是添加一个特判(虽然算法丑陋了许多),在AB,CD共线的情况下,判定二者是否相交。共线条件下判定是否相交很简单,不相交 $\Leftrightarrow$ 对于每条线段的每个端点(如A),其与另外一条线段的两个端点形成的两个向量(如AC,AD)同向。
代码实现及测试代码如下:
#include <iostream>
using namespace std;
struct Pos {
int x,y;
Pos(int X=-1,int Y=-1): x(X),y(Y){}
};
int xProduct(Pos A,Pos B,Pos C) {
return (B.x-A.x)*(C.y-A.y)-(C.x-A.x)*(B.y-A.y);
}
// Determin If vector AB and AC is in same direction
bool sameD(Pos A, Pos B, Pos C) {
return (B.x-A.x) * (C.x-A.x) + (B.y-A.y) * (C.y-A.y) > 0;
}
// Determine whether the line AB and CD intersect
bool cross(Pos A,Pos B,Pos C,Pos D) {
int cp_ABC = xProduct(A,B,C);
int cp_ABD = xProduct(A,B,D);
if (cp_ABC == 0 && cp_ABD == 0) {
return !(sameD(A, C, D) && sameD(B, C, D) && sameD(C, A, B));
}
return cp_ABC*cp_ABD<=0 && xProduct(C,D,A)*xProduct(C,D,B)<=0;
}
int main() {
bool ans;
// cross
ans = cross(Pos(0, 0), Pos(1, 1), Pos(0, 1), Pos(1, 0));
cout << "cross(1): " << ans << endl;
// Concurrent
ans = cross(Pos(0, 0), Pos(1, 1), Pos(0, 1), Pos(0, 0));
cout << "Concurrent(1): " << ans << endl;
// parallel
ans = cross(Pos(0, 0), Pos(0, 1), Pos(1, 0), Pos(1, 1));
cout << "parallel(0): " << ans << endl;
// not cross, not parallels
ans = cross(Pos(0, 0), Pos(0, 1), Pos(1, 0), Pos(1, 2));
cout << "not cross, not parallels(0): " << ans << endl;
// Collinear && Concurrent
ans = cross(Pos(0, 0), Pos(0, 1), Pos(0, 1), Pos(0, 2));
cout << "Collinear && Concurrent(1): " << ans << endl;
// wrong
// Collinear && not Concurrent
ans = cross(Pos(0, 0), Pos(0, 1), Pos(0, 2), Pos(0, 3));
cout << "Collinear && not Concurrent(0): " << ans << endl;
// ABC is corllinear but ABC, D is not corllinear
ans = cross(Pos(0, 0), Pos(0, 1), Pos(0, 2), Pos(1, 3));
cout << "ABC is corllinear but ABC, D is not corllinear(0): " << ans << endl;
// coincidence
ans = cross(Pos(0, 0), Pos(0, 1), Pos(0, 1), Pos(0, 0));
cout << "coincidence(1): " << ans << endl;
return 0;
}
程序运行结果如下:
cross(1): 1
Concurrent(1): 1
parallel(0): 0
not cross, not parallels(0): 0
Collinear && Concurrent(1): 1
Collinear && not Concurrent(0): 0
ABC is corllinear but ABC, D is not corllinear(0): 0
coincidence(1): 1